tayafluid.blogg.se - Quadratic graph

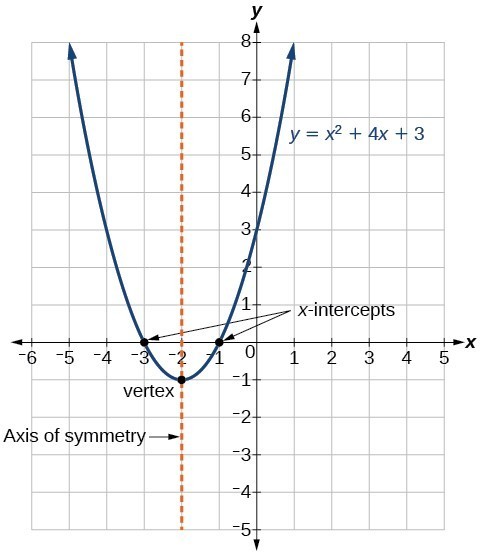
So the function with the highest |A| grows ( or falls, for A |2|, g(x) has a narrower graph. Its impact depends on |A| (magnitude of A). Coefficient A has a multiplying effect on the growth of x 2. The x 2 term grows faster than all the other terms combined. Between any two quadratic graphs, the one with a larger magnitude of A will be narrower. The width of a graph is a comparative feature. The graph intersects the x-axis at two points. In the graph below, the corresponding function has a positive discriminant. If the discriminant is zero, the graph will touch the x-axis at one point, so there is only one x-intercept. Discriminant of function f(x) = B 2 − 4AC = − 4.When the discriminant is negative, the graph will not touch the x-axis. ✩ Formula – Roots of a Quadratic Function If D If D = 0, graph just touches the x-axis and therefore only one x-intercept.The existence of roots depends on the sign of the discriminant D. You would have observed above that not all the graphs intersect the x-axis. The x-intercept is a point where a graph intersects the x-axis. On the y-axis, value of function equals the corresponding value of C.Īs C is the y-intercept, even the graphs of different quadratic functions with the same value of C will coincide on the y-axis. The graphs are shifted vertically (by the difference of respective C values).

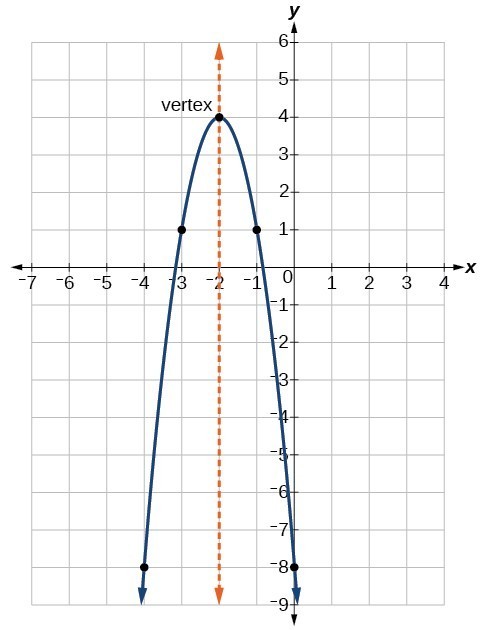
Similarly, the difference in y-values of h(x) and g(x) is 1 ( = 2 – 1 ). The difference in y-values of g(x) and f(x) is 2 ( = 1 – (-1) ). The graphs below show this shift using the following functions: If C is positive, the graph shifts up, and if C is negative, it shifts down. The value of C increases (or decreases, if C is negative) the value of the function. Therefore y-intercept is always equal to (0, C). So its y-coordinate is easy to calculate: The y-intercept is a point where the graph hits the y-axis. The axis of symmetry passes through x = -1 and is parallel to the y-axis. Using the formula above, you can calculate x and y values of the vertex as:

Axis of symmetry passes through it Exampleįind the vertex of a quadratic function y = x 2 + 2x + 1.

y-coordinate = f ( 2 A − B ) = 4 A 4 A C − B 2 .

It is the highest ( or maximum ) point when A 0 (upward graph).

It is symmetric across the vertical line passing through the vertex. There is only one vertex in a quadratic graph.

If A is negative, Ax 2 goes to -∞ (on either direction of x-axis).

If A is positive, Ax 2 goes to +∞ (on either direction of x-axis).

x 2 is always positive, so the sign of the term Ax 2 is determined by A.

The value of x 2 increases faster than all other terms combined.

On the x-axis, as we move away from the origin (either towards – ∞ or + ∞): Vertex is the highest point ( maximum value). Vertex is the lowest point ( minimum value).Ī (=-1) is negative, the graph is downwards. ExampleĪ (=1) is positive, the graph is upwards. It is upward or downward depending on the sign of the coefficient A. Where A, B, C are coefficients of a quadratic function in the standard form:īefore we graph a quadratic, let us understand these attributes.Ĭoefficient A determines the shape of the quadratic graph and its orientation. Graph trait Coefficients controlling the trait Upward A > 0 Downward A 0 Graph Width Magnitude of A The following table lists these traits and their relation to the coefficients. The coefficients of the quadratic function control these attributes. These are essential for graphing the quadratic function. The primary features of a quadratic graph are x and y-intercepts, vertex, and its orientation.

What are the attributes of these graphs? How can we use them in graphing the function? Attributes of a Quadratic Graph I will stop here.Some quadratic graphs are upwards, some downwards, some intersect with the x-axis, others not. The diagram shows that it fails the Horizontal Line Test, thus the inverse is not a function. I will not even bother applying the key steps above to find its inverse. I am sure that when I graph this, I can draw a horizontal line that will intersect it more than once. The first thing I realize is that this quadratic function doesn’t have a restriction on its domain. Switch the roles of \color + 2, if it exists.Key Steps in Finding the Inverse Function of a Quadratic Function